Exercises 1.31-1.60

All Exercises

Exercise 1.31 Convert the following decimal numbers to 8-bit sign/magnitude numbers or indicate that the decimal number would overflow the range

a) 42₁₀

b) −63₁₀

c) 124₁₀

d) −128₁₀

e) 133₁₀

Your answer: a) 42= b) −63= c) 124= d) −128= e) 133=

Solution:

a) 42₁₀ = 1x32(2⁵) + 0x16(2⁴) + 1x8(2³) + 0x4(2²) + 1x2(2¹) + 0x1(2⁰) = 0010 1010₂

b) −63₁₀ = 1x32(2⁵) + 1x16(2⁴) + 1x8(2³) + 1x4(2²) + 1x2(2¹) + 1x1(2⁰) = 1011 1111₂

c) 124₁₀ = 1x64(2⁶) + 1x32(2⁵) + 1x16(2⁴) + 1x8(2³) + 1x4(2²) + 0x2(2¹) + 0x1(2⁰) = 0111 1100₂

d) −128₁₀ = overflow

e) 133₁₀ = overflow

Exercise 1.32 Convert the following decimal numbers to 8-bit sign/magnitude numbers or indicate that the decimal number would overflow the range

a) 24₁₀

b) −59₁₀

c) 128₁₀

d) −150₁₀

e) 127₁₀

Your answer: a) 24= b) −59= c) 128= d) −150= e) 127=

Solution:

a) 24₁₀ = 0001 1000₂

b) −59₁₀ = 1011 1011₂

c) 128₁₀ = overflow

d) −150₁₀ = overflow

e) 127₁₀ = 0111 1111₂

Exercise 1.33 Convert the following 4-bit two's complement numbers to 8-bit two's complement numbers

a) 0101₂

b) 1010₂

Your answer: a) 0101= b) 1010=

Solution:

a) 0101₂ = 0000 0101₂

b) 1010₂ = 1111 1010₂

Exercise 1.34 Convert the following 4-bit two's complement numbers to 8-bit two's complement numbers

a) 0111₂

b) 1001₂

Your answer: a) 0111= b) 1001=

Solution:

a) 0111₂ = 0000 0111₂

b) 1001₂ = 1111 1001₂

Exercise 1.35 Repeat exercise 1.33 if the numbers are unsigned rather than two's complement

a) 0101₂

b) 1010₂

Your answer: a) 0101= b) 1010=

Solution:

a) 0101₂ = 0000 0101₂

b) 1010₂ = 0000 1010₂

Exercise 1.36 Repeat exercise 1.34 if the numbers are unsigned rather than two's complement

a) 0111₂

b) 1001₂

Your answer: a) 0111= b) 1001=

Solution:

a) 0111₂ = 0000 0111₂

b) 1001₂ = 0000 1001₂

Exercise 1.37 Base 8 is referred to as octal. Convert each of the numbers from exercise 1.25 to octal

a) 42₁₀

b) 63₁₀

c) 229₁₀

d) 845₁₀

Your answer: a) 42= b) 63= c) 229= d) 845=

Solution:

a) 42₁₀ = 5x8(8¹) + 2x1(8⁰) = 52₈

b) 63₁₀ = 7x8(8¹) + 7x1(8⁰) = 77₈

c) 229₁₀ = 3x64(8²) + 4x8(8¹) + 5x1(8⁰) = 345₈

d) 845₁₀ = 1x512(8³) + 5x64(8²) + 1x8(8¹) + 5x1(8⁰) = 1515₈

Exercise 1.38 Base 8 is referred to as octal. Convert each of the numbers from exercise 1.26 to octal

a) 14₁₀

b) 52₁₀

c) 339₁₀

d) 711₁₀

Your answer: a) 14= b) 52= c) 339= d) 711=

Solution:

a) 0o16

b) 0o64

c) 0o523

d) 0o1307

Exercise 1.39 Convert each of the following octal numbers to binary, hexadecimal, and decimal

a) 42₈

b) 63₈

c) 255₈

d) 3047₈

Your answer: a) 42= b) 63= c) 255= d) 3047=

Solution:

Convert Binary to Octal

Break a binary number into groups of 3 digits and convert each group separately. After that, just concatenate all the resulting octal digits.

a) 42₈ = 100 010₂ = 0010 0010₂ = 22₁₆ = 2x16 + 2 = 34₁₀

b) 63₈ = 110 011₂ = 0011 0011₂ = 33₁₆ = 3x16 + 3 = 51₁₀

c) 255₈ = 010 101 101₂ = 1010 1101₂ = AD₁₆ = 10x16 + 13 = 173₁₀

d) 3047₈ = 011 000 100 111₂ = 0110 0010 0111₂ = 627₁₆ = 6x256 + 2x16 + 7 = 1575₁₀

Exercise 1.40 Convert each of the following octal numbers to binary, hexadecimal, and decimal

a) 23₈

b) 45₈

c) 371₈

d) 2560₈

Your answer: a) 23= b) 45= c) 371= d) 2560=

Solution:

a) 0b10011; 0x13; 19

b) 0b100101; 0x25; 37

c) 0b11111001; 0xF9; 249

d) 0b10101110000; 0x570; 1392

Exercise 1.41 How many 5-bit two's complement numbers are greater than 0? How many are less than 0? How would your answer differ for sign/magnitude numbers?

Your answer: a) b) c)

Solution:

a) 15 greater than 0

b) 16 less than 0

c) 15 greater and 15 less for sign/magnitude

Exercise 1.42 How many 7-bit two's complement numbers are greater than 0? How many are less than 0? How would your answers differ for sign/magnitude numbers?

Your answer: a) b) c)

Solution:

a) (2⁶-1) are greater than 0 = 63

b) 2⁶ are less than 0 = 64

c) For sign/magnitude numbers, (2⁶-1)=63 are still greater than 0, but (2⁶-1)=63 are less than 0

Exercise 1.43 How many bytes are in a 32-bit word? How many nibbles are in the word?

Your answer: a) b)

Solution:

a) 4

b) 8

Exercise 1.44 How many bytes are in a 64-bit word?

Your answer:

Solution:

8

Exercise 1.45 A particular DSL modem operates at 768 kbit/sec. How many bytes can it receive in 1 minute?

Your answer: 768kbit/sec =

Solution:

5760000

Exercise 1.46 USB 3.0 can send data at 5Gbits/sec. How many bytes can it send in 1 minute?

Your answer: 5Gbits/sec =

Solution:

(5×10⁹ bits/second)(60 seconds/minute)(1 byte/8 bits) = 3.75×10¹⁰ bytes

Exercise 1.47 Hard disk manufacturers use the term "megabyte" to mean 10⁶ bytes and "gigabyte" to mean 10⁹ bytes. How many real GBs of music you can store on a 50GB hard disk?

Your answer: 50GB =

Solution:

50x10⁹/2³⁰=50 000 000 000 / 1 073 741 824 = 46.566 GBytes

tip

2¹⁰ = 1024 ≈ 10³ bytes (1 KBytes)

2²⁰ = 1 048 578 ≈ 10⁶ bytes (1 MBytes)

2³⁰ = 1 073 741 824 ≈ 10⁹ bytes (1 GBytes)

Exercise 1.48 Estimate the value of 2³¹

Your answer: 2^31=

Solution:

2³¹=2³⁰x2¹
2³⁰ ≈ 1x10⁹ ≈ 1 000 000 000
So 2³¹ ≈ 2 000 000 000

Exercise 1.49 A memory on the Pentium II microprocessor is organized as a rectangular array of bits with 2⁸ rows and 2⁹ columns. Estimate how many bits it has without using a calculator?

Your answer: 2^8x2^9=

Solution:

2⁸ x 2⁹ = 2¹⁷ = 2¹⁰ + 2⁷ = 1 Kbits x 128 = 128 Kbits

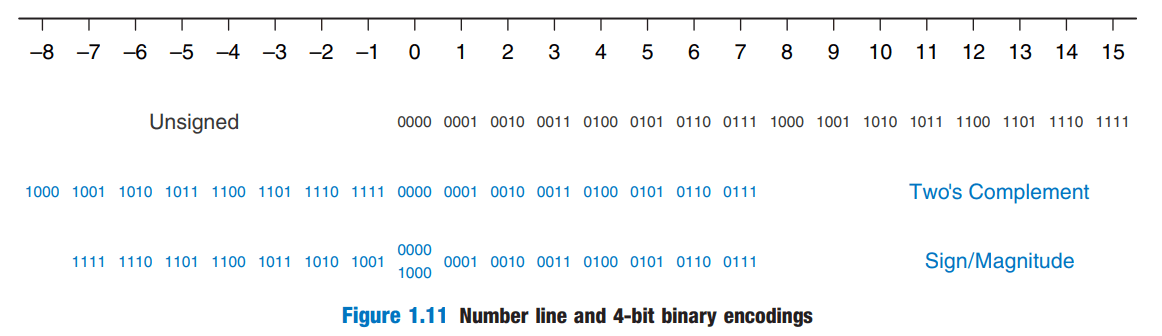
Exercise 1.50 Draw a number line analogous to Figure 1.11 (see below) for 3-bit unsigned, two's complement, and sign/magnitude numbers

Your answer:

Solution:

	-4	-3	-2	-1	0	1	2	3	4	5	6	7
un					000	001	010	011	100	101	110	111
two	100	101	110	111	000	001	010	011
S/M		111	110	101	000 100	001	010	011

Exercise 1.51 Draw a number line analogous to Figure 1.11 for 2-bit unsigned, two's complement, and sign/magnitude numbers

Your answer:

Solution:

	-2	-1	0	1	2	3
unsigned			00	01	10	11
two's	10	11	00	01
Sign/M		11	00 10	01

Exercise 1.52 Perform the following additions of unsigned binary numbers. Indicate whether or not the sum overflows a 4-bit result

a) 1001₂ + 0100₂

b) 1101₂ + 1011₂

Your answer: a) 1001 + 0100 = b) 1101 + 1011 =

Solution:

a) 1101

  1001
+ 0100
  ====
  1101   

b) 11110 (overflow)

  1101
+ 1011
  ====
1 1000  <- overflow

Unsigned Numbers

When the msb (most significant bit) is carried out, it's an overflow. For unsigned numbers.

Exercise 1.53 Perform the following additions of unsigned binary numbers. Indicate whether or not the sum overflows an 8-bit result

a) 10011001₂ + 01000100₂

b) 11010010₂ + 10110110₂

Your answer: a) 10011001 + 01000100 = b) 11010010 + 10110110 =

Solution:

a) 11011101

  10011001
+ 01000100
  ========
  11011101

b) 110001000 (overflow)

  11010010
+ 10110110
  ========
1 10001000  <- overflow

Exercise 1.54 Repeat exercise 1.52, assuming that the binary numbers are in two's complement form

a) 1001₂ + 0100₂

b) 1101₂ + 1011₂

Your answer: a) 1001 + 0100 = b) 1101 + 1011 =

Solution:

a) 1101 (no overflow)

  1001
+ 0100
  ====
  1101 (-8+4+1)=-3  

Two's complement numbers

Overflow never occurs when adding two numbers with different signs

b) 1000 (no overflow)

  1101 = -3
+ 1011 = -5
  ====
1 1000 <- carry discarded
  1000 -> result: -8

Two's Complement Numbers

When adding numbers in the two's complement form, the carry out from msb is discarding. See two's complement overflow

danger

Unlike unsigned numbers, a carry out of the most significant column does not indicate overflow

tip

Instead, overflow occurs if the two numbers being added have the same sign bit and the result has the opposite sign bit.

Exercise 1.55 Repeat exercise 1.53, assuming that the binary numbers are in two's complement form

a) 10011001₂ + 01000100₂

b) 11010010₂ + 10110110₂

Your answer: a) 10011001 + 01000100 = b) 11010010 + 10110110 =

Solution:

a) 11011101

  10011001
+ 01000100
  ========
  11011101

b) 10001000

  11010010
+ 10110110
  ========
1 10001000  <- no overflow
  10001000  -> result

Exercise 1.56 Convert the following decimal numbers to 6-bit two's complement binary numbers and add them. Indicate whether or not the sum overflows a 6-bit result

a) 16₁₀+ 9₁₀

b) 27₁₀ + 31₁₀

c) −4₁₀ + 19₁₀

d) 3₁₀ + −32₁₀

e) −16₁₀ + −9₁₀

f) −27₁₀ + −31₁₀

Your answer: a) 16 + 9 = b) 27 + 31 = c) −4 + 19 = d) 3 + −32 = e) −16 + −9 = f) −27 + −31 =

Solution:

a) 010000 + 001001 = 011001

   010000
+  001001
   ======
   011001 = 25

b) 011011 + 011111 = 111010 (overflow)

   011011 = 16+8+2+1=27
+  011111 = 16+8+4+2+1=31
   ======
   111010 <- sign bit changed (overflow)
   result: -32+16+8+2=-6

c) 111100 + 010011 = 001111

   111100
+  010011
   ======
 1 001111 -> discard carry
   001111 = 15

d) 000011 + 100000 = 100011

   000011
+  100000
   ======
   100011 = -32+2+1=-29

e) 110000 + 110111 = 100111

   110000 = -32+16=-16
+  110111 = -32+16+4+2+1=-9
   ======
 1 100111 -> discard carry
   100111 = -32+4+2+1=-25

f) 100101 + 100001 = 000110 (overflow)

   100101 = -32+4+1=-27
+  100001 = -32+1=-31
   ======
 1 000110 -> discard carry
   000110 -> changed msb
   overflow!

Exercise 1.57 Repeat exercise 1.56 for the following numbers

a) 7₁₀ + 13₁₀

b) 17₁₀ + 25₁₀

c) −26₁₀ + 8₁₀

d) 31₁₀ + −14₁₀

e) −19₁₀ + −22₁₀

f) −2₁₀ + −29₁₀

Your answer: a) 7 + 13 = b) 17 + 25 = c) −26 + 8 = d) 31 + −14 = e) −19 + −22 = f) −2 + −29 =

Solution:

a) 000111 + 001101 = 010100

000111 7
001101 13
======
010100

b) 010001 + 011001 = 101010, overflow

010001 17
011001 25
======
101010 -> overflow

c) 100110 + 001000 = 101110

100110 -26
001000  8
======
101110

d) 011111 + 110010 = 010001

 011111 31
 110010 -14
 ======
1010001
 010001

e) 101101 + 101010 = 010111, overflow

 101101 -19
 101010 -22
 ======
1010111
 010111 -> overflow

f) 111110 + 100011 = 100001

 111110 -2
 100011 -29
 ======
1100001
 100001 = -31

Exercise 1.58 Perform the following additions of unsigned hexadecimal numbers. Indicate whether or not the sum overflows an 8-bit (two hex digit) result

a) 7₁₆ + 9₁₆

b) 13₁₆ + 28₁₆

c) AB₁₆ + 3E₁₆

d) 8F₁₆ + AD₁₆

Your answer: a) 7 + 9 = b) 13 + 28 = c) AB + 3E = d) 8F + AD =

Solution:

a) 7 + 9 = 10₁₆

 0111 
 1001
 ====
10000

b) 13 + 28 = 3B

0001 0011
0010 1000
=========
0011 1011

c) AB + 3E = E9

1010 1011
0011 1110
=========
1110 1001

d) 8F + AD = 13С (overflow)

 1000 1111
 1010 1101
 =========
10011 1100 -> overflow

Exercise 1.59 Perform the following additions of unsigned hexadecimal numbers. Indicate whether or not the sum overflows an 8-bit (two hex digit) result

(a) 22₁₆ + 8₁₆

(b) 73₁₆ + 2C₁₆

(c) 7F₁₆ + 7F₁₆

(d) C2₁₆ + A4₁₆

Your answer: (a) 22 + 8 = (b) 73 + 2C = (c) 7F + 7F = (d) C2 + A4 =

Solution:

a) 22 + 8 = 0x2A

0010 0010
0000 1000
=========
0010 1010

b) 73 + 2C = 0x9F

0111 0011
0010 1100
=========
1001 1111

c) 7F + 7F = 0xFE

0111 1111
0111 1111
=========
1111 1110

d) C2 + A4 = 0x166, overflow

 1100 0010
 1010 0100
 =========
10110 0110

Exercise 1.60 Convert the following decimal numbers to 5-bit two's complement binary numbers and subtract them. Indicate whether or not the difference overflows a 5-bit result

a) 9₁₀ − 7₁₀

b) 12₁₀ − 15₁₀

c) −6₁₀ − 11₁₀

d) 4₁₀ − −8₁₀

Your answer: a) 9 − 7 = b) 12 − 15 = c) −6 − 11 = d) 4 − −8 =

Solution:

a) 9 - 7 = 01001 - 00111 = 00010

   01001 9
+  11001 -7
   =====
 1 00010 <- carry discarded 

b) 12 -15 = 01100 - 01111 = 11101

   01100 12    01100 12
-  01111 15  + 10001 -15
   =====       =====
   11101   =   11101

c) −6 − 11 = 11010 - 01011 = 01111 (overflow)

  11010 -6     11010  -6
+ 10101 -11  - 01011  11
  =====        =====
1 01111 15     10111  -9
   
   both error !! overflow

d) 4 − −8 = 00100 - 11000 = 01100

  00100 4   00100 4
+ 01000 8   10111
  =====     +   1
  01100   - 11000 -8
            =====
          1 01100 12 <- carry discard

All Exercises